Name

besseli — Modified Bessel functions of the first kind (I sub alpha).

besselj — Bessel functions of the first kind (J sub alpha).

besselk — Modified Bessel functions of the second kind (K sub alpha).

bessely — Bessel functions of the second kind (Y sub alpha).

besselh — Bessel functions of the third kind (aka Hankel functions)

Calling Sequence

y = besseli(alpha,x [,ice])
y = besselj(alpha,x [,ice])
y = besselk(alpha,x [,ice])
y = bessely(alpha,x [,ice])
y = besselh(alpha,x)
y = besselh(alpha,K,x [,ice])

Parameters

x

real or complex vector.

alpha

real vector

ice

integer flag, with default value 0

K

integer, with possible values 1 or 2, the Hankel function type.

Description

Warning: the semantics of these functions changes between Scilab-3.0 and Scilab-3.1. The old semantics is available for compatibility using the oldbesseli, oldbesselj, oldbesselk, oldbessely functions.

  • besseli(alpha,x) computes modified Bessel functions of the first kind (I sub alpha), for real order alpha and argument x. besseli(alpha,x,1) computes besseli(alpha,x).*exp(-abs(real(x))).

  • besselj(alpha,x) computes Bessel functions of the first kind (J sub alpha), for real order alpha and argument x. besselj(alpha,x,1) computes besselj(alpha,x).*exp(-abs(imag(x))).

  • besselk(alpha,x) computes modified Bessel functions of the second kind (K sub alpha), for real order alpha and argument x. besselk(alpha,x,1) computes besselk(alpha,x).*exp(x).

  • bessely(alpha,x) computes Bessel functions of the second kind (Y sub alpha), for real order alpha and argument x. bessely(alpha,x,1) computes bessely(alpha,x).*exp(-abs(imag(x))).

  • besselh(alpha [,K] ,x) computes Bessel functions of the third kind (Hankel function H1 or H2 depending on K), for real order alpha and argument x. If omitted K is supposed to be equal to 1. besselh(alpha,1,x,1) computes besselh(alpha,1,x).*exp(-%i*x) and besselh(alpha,2,x,1) computes besselh(alpha,2,x).*exp(%i*x)

Remarks

If alpha and x are arrays of the same size, the result y is also that size. If either input is a scalar, it is expanded to the other input's size. If one input is a row vector and the other is a column vector, the resulty is a two-dimensional table of function values.

Y_alpha and J_alpha Bessel functions are 2 independant solutions of the Bessel 's differential equation :

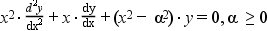
K_alpha and I_alpha modified Bessel functions are 2 independant solutions of the modified Bessel 's differential equation :

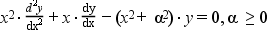
H^1_alpha and H^2_alpha, the Hankel functions of first and second kind, are linear linear combinations of Bessel functions of the first and second kinds:

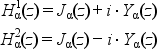
Examples

 
//  besselI functions
// ==================
   x = linspace(0.01,10,5000)';
   clf()
   subplot(2,1,1)
   plot2d(x,besseli(0:4,x), style=2:6)
   legend('I'+string(0:4),2);
   xtitle("Some modified Bessel functions of the first kind")
   subplot(2,1,2)
   plot2d(x,besseli(0:4,x,1), style=2:6)
   legend('I'+string(0:4),1);
   xtitle("Some modified scaled Bessel functions of the first kind")

// besselJ functions
// =================
   x = linspace(0,40,5000)';
   clf()
   plot2d(x,besselj(0:4,x), style=2:6, leg="J0@J1@J2@J3@J4")
   legend('I'+string(0:4),1);
   xtitle("Some Bessel functions of the first kind")

// use the fact that J_(1/2)(x) = sqrt(2/(x pi)) sin(x)
// to compare the algorithm of besselj(0.5,x) with a more direct formula 
   x = linspace(0.1,40,5000)';
   y1 = besselj(0.5, x);
   y2 = sqrt(2 ./(%pi*x)).*sin(x);
   er = abs((y1-y2)./y2);
   ind = find(er > 0 & y2 ~= 0);
   clf()
   subplot(2,1,1)
   plot2d(x,y1,style=2)
   xtitle("besselj(0.5,x)")
   subplot(2,1,2)
   plot2d(x(ind), er(ind), style=2, logflag="nl")
   xtitle("relative error between 2 formulae for besselj(0.5,x)") 

// besselK functions
// =================
   x = linspace(0.01,10,5000)';
   clf()
   subplot(2,1,1)
   plot2d(x,besselk(0:4,x), style=0:4, rect=[0,0,6,10])
   legend('K'+string(0:4),1);
   xtitle("Some modified Bessel functions of the second kind")
   subplot(2,1,2)
   plot2d(x,besselk(0:4,x,1), style=0:4, rect=[0,0,6,10])
   legend('K'+string(0:4),1);
   xtitle("Some modified scaled Bessel functions of the second kind")

// besselY functions
// =================
   x = linspace(0.1,40,5000)'; // Y Bessel functions are unbounded  for x -> 0+
   clf()
   plot2d(x,bessely(0:4,x), style=0:4, rect=[0,-1.5,40,0.6])
   legend('Y'+string(0:4),4);
   xtitle("Some Bessel functions of the second kind")

// besselH functions
// =================
   x=-4:0.025:2; y=-1.5:0.025:1.5;
   [X,Y] = ndgrid(x,y);
   H = besselh(0,1,X+%i*Y); 
   clf();f=gcf();
   xset("fpf"," ")
   f.color_map=jetcolormap(16);
   contour2d(x,y,abs(H),0.2:0.2:3.2,strf="034",rect=[-4,-1.5,3,1.5])
   legends(string(0.2:0.2:3.2),1:16,"ur")
   xtitle("Level curves of |H1(0,z)|")

Authors

Amos, D. E., (SNLA)
Daniel, S. L., (SNLA)
Weston, M. K., (SNLA)

Used Functions

The source codes can be found in SCI/modules/special_functions/src/fortran/slatec and SCI/modules/special_functions/src/fortran

Slatec : dbesi.f, zbesi.f, dbesj.f, zbesj.f, dbesk.f, zbesk.f, dbesy.f, zbesy.f, zbesh.f

Drivers to extend definition area (Serge Steer INRIA): dbesig.f, zbesig.f, dbesjg.f, zbesjg.f, dbeskg.f, zbeskg.f, dbesyg.f, zbesyg.f, zbeshg.f