Parameters

Description

pr=binomial(p,n) returns the binomial probability vector, i.e. pr(k+1) is the probability of k success in n independent Bernouilli trials with probability of success p. In other words : pr(k+1) = probability(X=k) , with X a random variable following the B(n,p) distribution, and numerically :

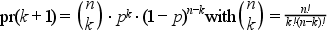
Examples

 
// first example
n=10;p=0.3; clf(); plot2d3(0:n,binomial(p,n));

// second example 
n=50;p=0.4;
mea=n*p; sigma=sqrt(n*p*(1-p));
x=( (0:n)-mea )/sigma;
clf()
plot2d(x, sigma*binomial(p,n));
deff('y=Gauss(x)','y=1/sqrt(2*%pi)*exp(-(x.^2)/2)')
plot2d(x, Gauss(x), style=2);

// by binomial formula (Caution if big n)
function pr=binomial2(p,n)
x=poly(0,'x');pr=coeff((1-p+x)^n).*horner(x^(0:n),p);
endfunction
p=1/3;n=5;
binomial(p,n)-binomial2(p,n)

// by Gamma function: gamma(n+1)=n! (Caution if big n)
p=1/3;n=5;
Cnks=gamma(n+1)./(gamma(1:n+1).*gamma(n+1:-1:1));
x=poly(0,'x');
pr=Cnks.*horner(x.^(0:n).*(1-x)^(n:-1:0),p);
pr-binomial(p,n)
 

See Also