Calling Sequence
y = oldbesseli(alpha,x) y = oldbesseli(alpha,x,ice) y = oldbesselj(alpha,x) y = oldbesselk(alpha,x) y = oldbesselk(alpha,x,ice) y = oldbessely(alpha,x)
Parameters
- x
real vector with non negative entries
- alpha
real vector with non negative entries regularly spaced with increment equal to one
alpha=alpha0+(n1:n2)- ice
integer flag, with default value 1
Description
These functions are obsolete, use besseli, besselj, besselk, bessely instead. Note however that the semantics of these two sets of functions are different.
oldbesseli(alpha,x) computes modified Bessel
functions of the first kind (I sub alpha), for real, non-negative order
alpha and real non negative argument
x. besseli(alpha,x,2) computes
besseli(alpha,x).*exp(-x).
oldbesselj(alpha,x) computes Bessel functions of
the first kind (J sub alpha), for real, non-negative order
alpha and real non negative argument
x.
oldbesselk(alpha,x) computes modified Bessel
functions of the second kind (K sub alpha), for real, non-negative order
alpha and real non negative argument
x. besselk(alpha,x,2) computes
besselk(alpha,x).*exp(x).
oldbessely(alpha,x) computes Bessel functions of
the second kind (Y sub alpha), for real, non-negative order
alpha and real non negative argument
x.
alpha and x may be vectors.
The output is m-by-n with m
= size(x,'*'), n = size(alpha,'*') whose
(i,j) entry is
oldbessel?(alpha(j),x(i)).
Remarks
Y_alpha and J_alpha Bessel functions are 2 independant solutions of the Bessel 's differential equation :
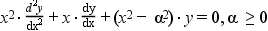
K_alpha and I_alpha modified Bessel functions are 2 independant solutions of the modified Bessel 's differential equation :
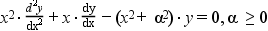
Examples
// example #1: display some I Bessel functions
x = linspace(0.01,10,5000)';
y = oldbesseli(0:4,x);
ys = oldbesseli(0:4,x,2);
clf()
subplot(2,1,1)
plot2d(x,y, style=2:6, leg="I0@I1@I2@I3@I4", rect=[0,0,6,10])
xtitle("Some modified Bessel functions of the first kind")
subplot(2,1,2)
plot2d(x,ys, style=2:6, leg="I0s@I1s@I2s@I3s@I4s", rect=[0,0,6,1])
xtitle("Some modified scaled Bessel functions of the first kind")
// example #2 : display some J Bessel functions
x = linspace(0,40,5000)';
y = besselj(0:4,x);
clf()
plot2d(x,y, style=2:6, leg="J0@J1@J2@J3@J4")
xtitle("Some Bessel functions of the first kind")
// example #3 : use the fact that J_(1/2)(x) = sqrt(2/(x pi)) sin(x)
// to compare the algorithm of besselj(0.5,x) with
// a more direct formula
x = linspace(0.1,40,5000)';
y1 = besselj(0.5, x);
y2 = sqrt(2 ./(%pi*x)).*sin(x);
er = abs((y1-y2)./y2);
ind = find(er > 0 & y2 ~= 0);
clf()
subplot(2,1,1)
plot2d(x,y1,style=2)
xtitle("besselj(0.5,x)")
subplot(2,1,2)
plot2d(x(ind), er(ind), style=2, logflag="nl")
xtitle("relative error between 2 formulae for besselj(0.5,x)")
// example #4: display some K Bessel functions
x = linspace(0.01,10,5000)';
y = besselk(0:4,x);
ys = besselk(0:4,x,1);
clf()
subplot(2,1,1)
plot2d(x,y, style=0:4, leg="K0@K1@K2@K3@K4", rect=[0,0,6,10])
xtitle("Some modified Bessel functions of the second kind")
subplot(2,1,2)
plot2d(x,ys, style=0:4, leg="K0s@K1s@K2s@K3s@K4s", rect=[0,0,6,10])
xtitle("Some modified scaled Bessel functions of the second kind")
// example #5: plot severals Y Bessel functions
x = linspace(0.1,40,5000)'; // Y Bessel functions are unbounded for x -> 0+
y = bessely(0:4,x);
clf()
plot2d(x,y, style=0:4, leg="Y0@Y1@Y2@Y3@Y4", rect=[0,-1.5,40,0.6])
xtitle("Some Bessel functions of the second kind")