Nom
PDE — 1D PDE block
Description
This block is an implementation of several numerical schemes (Finite Elements (1st and 2nd order), Finite Differences (1st and 2nd order), Finite Volumes (1st order)) to solve mono dimensional PDE (Partial Differential Equation) within SCICOS. The mathematical framwork was restricts in PDEs linear scalars with maximum order 2 in time and space. The goal is to provide engineers and physicists with an easy to use toolbox in SCICOS that will let them graphically describe the PDE to be solved. A decision system selects the most efficient numerical scheme depending on the type of the PDE and runs the solvers.
Dialog box
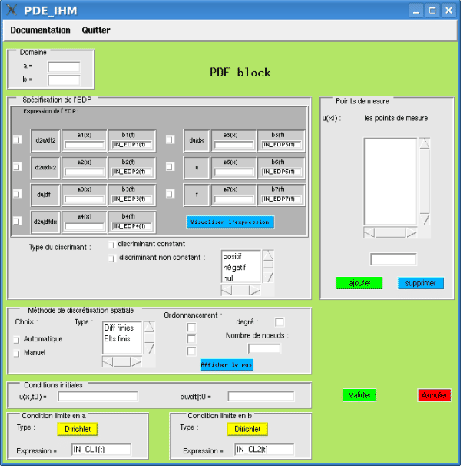
a et b
(double) The two edges of the discretization field.
specification de l'EDP
check box to select the PDE operators. ai(x), bi(t) (i=1:7) are the operator coefficients. type of PDE discriminant (constant or variable, in the later case, the sign should be given)
Discretization methode
choix (check box) : is the choice for the manual or the automatic mode. type : in the manual mode we can give the method type (Finite differences, finite elements or finite volumes). degré : method degre (1 or 2 for the FD and FE methods, 1 for the FV method). Nombre de noeuds : to give the number of the nodal points.
Conditions initiales
u(x,t0)=, du/dt at t0= : to give the initial conditions.
Conditions aux limites
type : two type of the boundray conditions are possible : Dirichlet or Neumann. expressions : to give then boundray conditions expressions.
Points de mesures
To give the list of mesurment points.
Name
A getvalue box to give the block name's.
Default properties
always active: yes
direct-feedthrough: no
zero-crossing: no
mode: no
regular inputs:
- port 1 : size [1,1] / type 1
- port 2 : size [1,1] / type 0
- port 3 : size [1,1] / type 0
- port 4 : size [1,1] / type 0
- port 5 : size [1,1] / type 1
regular outputs:
- port 1 : size [10,1] / type 1
- port 2 : size [0,1] / type 1
number/sizes of activation inputs: 0
number/sizes of activation outputs: 0
continuous-time state: yes
discrete-time state: no
object discrete-time state: no
name of computational function: PDE
