Name
qpsolve — linear quadratic programming solver
Calling Sequence
[x [,iact [,iter [,f]]]]=qpsolve(Q,p,C,b,ci,cs,me)
Parameters
- Q
real positive definite symmetric matrix (dimension
n x n).- p
real (column) vector (dimension
n)- C
real matrix (dimension
(me + md) x n). This matrix may be dense or sparse.- b
RHS column vector (dimension
m=(me + md))- ci
column vector of lower-bounds (dimension
n). If there are no lower bound constraints, putci = []. If some components ofxare bounded from below, set the other (unconstrained) values ofcito a very large negative number (e.g.ci(j) = -number_properties('huge').- cs
column vector of upper-bounds. (Same remarks as above).
- me
number of equality constraints (i.e.
C(1:me,:)*x = b(1:me))- x
optimal solution found.
- iact
vector, indicator of active constraints. The first non zero entries give the index of the active constraints
- iter
. 2x1 vector, first component gives the number of "main" iterations, the second one says how many constraints were deleted after they became active.
Description
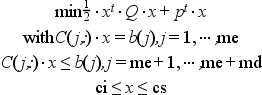
This function requires Q to be symmetric positive
definite. If that hypothesis is not satisfied, one may use the quapro
function, which is provided in the Scilab quapro toolbox.
The qpsolve solver is implemented as a Scilab script, which calls the compiled qp_solve primitive. It is provided as a facility, in order to be a direct replacement for the former quapro solver : indeed, the qpsolve solver has been designed so that it provides the same interface, that is, the same input/output arguments. But the x0 and imp input arguments are available in quapro, but not in qpsolve.
Examples
//Find x in R^6 such that:
//C1*x = b1 (3 equality constraints i.e me=3)
C1= [1,-1,1,0,3,1;
-1,0,-3,-4,5,6;
2,5,3,0,1,0];
b1=[1;2;3];
//C2*x <= b2 (2 inequality constraints)
C2=[0,1,0,1,2,-1;
-1,0,2,1,1,0];
b2=[-1;2.5];
//with x between ci and cs:
ci=[-1000;-10000;0;-1000;-1000;-1000];
cs=[10000;100;1.5;100;100;1000];
//and minimize 0.5*x'*Q*x + p'*x with
p=[1;2;3;4;5;6]; Q=eye(6,6);
//No initial point is given;
C=[C1;C2];
b=[b1;b2];
me=3;
[x,iact,iter,f]=qpsolve(Q,p,C,b,ci,cs,me)
//Only linear constraints (1 to 4) are active
See Also
optim, qp_solve, qldThe contributed toolbox "quapro" may also be of interest, in
particular for singular Q.
Memory requirements
Let r be
r=min(m,n)
Then the memory required by qpsolve during the computations is
2*n+r*(r+5)/2 + 2*m +1
Authors
- S. Steer
INRIA (Scilab interface)
- Berwin A. Turlach
School of Mathematics and Statistics (M019), The University of Western Australia, Crawley, AUSTRALIA (solver code)
References
Goldfarb, D. and Idnani, A. (1982). "Dual and Primal-Dual Methods for Solving Strictly Convex Quadratic Programs", in J.P. Hennart (ed.), Numerical Analysis, Proceedings, Cocoyoc, Mexico 1981, Vol. 909 of Lecture Notes in Mathematics, Springer-Verlag, Berlin, pp. 226-239.
Goldfarb, D. and Idnani, A. (1983). "A numerically stable dual method for solving strictly convex quadratic programs", Mathematical Programming 27: 1-33.
QuadProg (Quadratic Programming Routines), Berwin A Turlach,http://www.maths.uwa.edu.au/~berwin/software/quadprog.html